
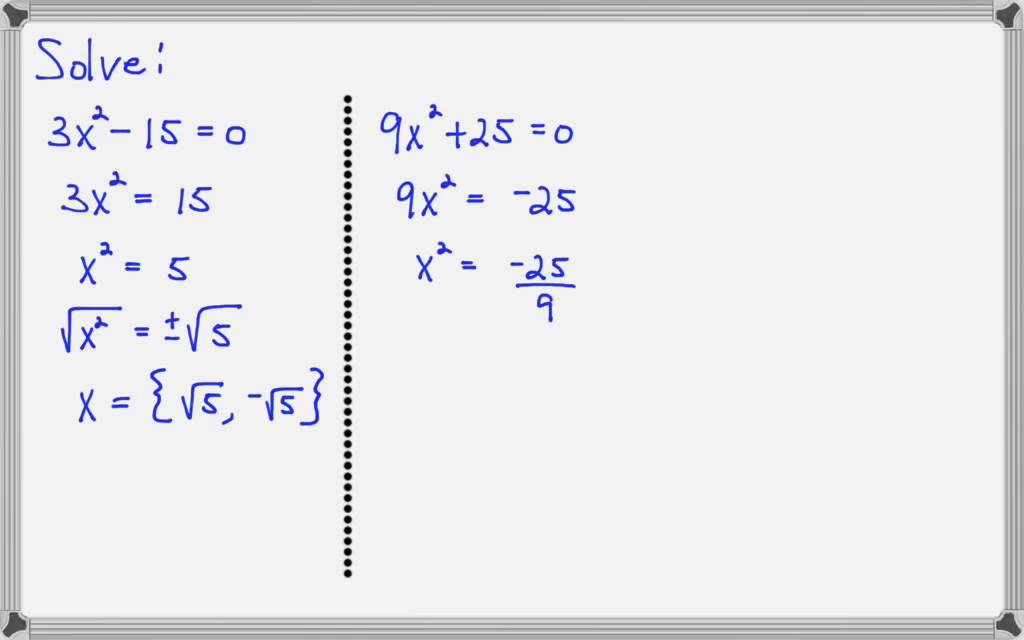
Now calculate ( – b + root_part ) / denom and store it in root1 and ( – b – root_part ) / denom in root2. In other words, the roots of a quadratic equation are the values of 'x' where the graph of. The quadratic equations having discriminant values lesser than zero b2 4ac < 0, converted by the use i2 1, to obtain the complex roots. The roots of a quadratic equation are the values of 'x' in the equation for which the equation holds true. The square root of a negative number is not possible and hence we convert it to a complex number. So lets calculate square root of b 2 – 4 * a * c and store it in variable root_part. Complex roots are the imaginary roots of quadratic equations that are represented as complex numbers. To calculate the roots of a quadratic equation in a C program, we need to break down the formula and calculate smaller parts of it and then combine to get the actual solution. Print("Two Distinct Complex Roots Exists: root1 = %.2f+%.2f and root2 = %.2f-%.YouTube Link: In the example below, a function called roots is created which takes a, b and c as arguments to calculate the.


Imaginary = math.sqrt(-discriminant) / (2 * a) Example: Calculate roots of a Quadratic equation. Print("Two Equal and Real Roots Exists: root1 = %.2f and root2 = %.2f" %(root1, root2)) Print("Two Distinct Real Roots Exists: root1 = %.2f and root2 = %.2f" %(root1, root2)) Root2 = (-b - math.sqrt(discriminant) / (2 * a)) This is a quadratic equation with roots 2 and 5. Now if x 2 and x 5 are the solutions then the equation could have been factorised as (x 2)(x 5) 0. Roots of the Quadratic Equations A root of the quadratic equation ax² + bc + c 0 is a number (real or complex) such that a a²+ba+c0 then (x-a) is factor of ax²+bx+c. For example, the roots of the quadratic equation x2 - 7x + 10 0 are x 2 and x 5 because they satisfy the equation. steps for solving a quadratic equation but in reverse order. They are also known as the 'solutions' or 'zeros' of the quadratic equation. Although it is usually in the Further Mathematics syllabus it is well within the reach of any A Level Mathematics candidate and only involves a very simple extension of the ideas in the A level Mathematics syllabus. The roots of a quadratic equation are the values of the variable that satisfy the equation. Root1 = (-b + math.sqrt(discriminant) / (2 * a)) This lesson concentrates on the relationship between the roots and the coefficients of a Quadratic Equation. Here, b 2 - 4ac called as the discriminant (which is denoted by D) of the quadratic equation, decides the nature of. ax 2 + bx + c 0 (where a, b, and c are real numbers and a 0) We can find the roots of the quadratic equation using the formula, x -b ± (b 2 - 4ac)/2a.
#ROOTS OF QUADRATIC EQUATION PDF#


 0 kommentar(er)
0 kommentar(er)
